Navigation Structure
Table of contents
Load dataset:
dat <- read.table("uk_ipip300_data1.csv", sep = ";", header = TRUE)
Library
library(lavaan)
## This is lavaan 0.6-9
## lavaan is FREE software! Please report any bugs.
Assumption testing
Test for multivariate normality
First: new dataset with variables of interest.
library(MVN)
extra.labels <- c("Opene_1", "Opene_2", "Opene_3", "Opene_4",
"Agree_1", "Agree_2", "Agree_3", "Agree_4",
"Neuro_1", "Neuro_2", "Neuro_3", "Neuro_4")
dat.extra <- na.omit(dat[,extra.labels])
# MVN command for QQ-Plot, Normality tests
mvn(dat.extra, mvnTest = c("mardia"), multivariatePlot = "qq", desc = F, showOutliers=T, showNewData=F)
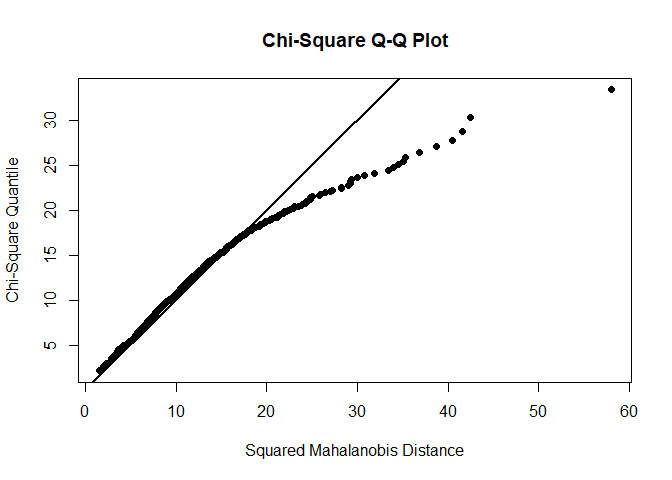
## $multivariateNormality
## Test Statistic p value Result
## 1 Mardia Skewness 1244.98550356253 9.57858038202079e-97 NO
## 2 Mardia Kurtosis 12.7621671073881 0 NO
## 3 MVN <NA> <NA> NO
##
## $univariateNormality
## Test Variable Statistic p value Normality
## 1 Anderson-Darling Opene_1 21.1669 <0.001 NO
## 2 Anderson-Darling Opene_2 23.5159 <0.001 NO
## 3 Anderson-Darling Opene_3 18.9456 <0.001 NO
## 4 Anderson-Darling Opene_4 44.2574 <0.001 NO
## 5 Anderson-Darling Agree_1 43.6023 <0.001 NO
## 6 Anderson-Darling Agree_2 39.9714 <0.001 NO
## 7 Anderson-Darling Agree_3 39.9981 <0.001 NO
## 8 Anderson-Darling Agree_4 47.9344 <0.001 NO
## 9 Anderson-Darling Neuro_1 19.3713 <0.001 NO
## 10 Anderson-Darling Neuro_2 25.3773 <0.001 NO
## 11 Anderson-Darling Neuro_3 20.8063 <0.001 NO
## 12 Anderson-Darling Neuro_4 21.7073 <0.001 NO
##
## $multivariateOutliers
## NULL
Second: Check outliers.
See here how to check for outliers (Leverage / Influence).
Simple SEM model
Specify model
~ regressed on
=~ is measured by for latent construct
~~ covariance
Regress some simple paths in the example:
model <- '
#constructs
op =~ Opene_1 + Opene_2 + Opene_3 + Opene_4
ag =~ Agree_1 + Agree_2 + Agree_3 + Agree_4
ne =~ Neuro_1 + Neuro_2 + Neuro_3 + Neuro_4
#paths
ag ~ ne
op ~ ne + ag'
Can use different se. For example, se = “robust” or se=“bootstrap”, bootstrap=5000.
Can use different estimators, default is estimator = “ML”, alternately use estimator = MLM or MLR for incomplete datasets.
MLM –> maximum likelihood estimation with robust standard errors and a Satorra-Bentler scaled test statistic. For complete data only.
MLR –> maximum likelihood estimation with robust (Huber-White) standard errors and a scaled test statistic that is (asymptotically) equal to the Yuan-Bentler test statistic. For both complete and incomplete data.
Fit and summary
fit <- cfa(model, data=dat, estimator="MLM", std.lv=TRUE)
summary(fit, fit.measures=T, standardized=T, rsquare=T)
## lavaan 0.6-9 ended normally after 29 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 27
##
## Used Total
## Number of observations 583 600
##
## Model Test User Model:
## Standard Robust
## Test Statistic 201.116 184.729
## Degrees of freedom 51 51
## P-value (Chi-square) 0.000 0.000
## Scaling correction factor 1.089
## Satorra-Bentler correction
##
## Model Test Baseline Model:
##
## Test statistic 1111.634 1002.792
## Degrees of freedom 66 66
## P-value 0.000 0.000
## Scaling correction factor 1.109
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.856 0.857
## Tucker-Lewis Index (TLI) 0.814 0.815
##
## Robust Comparative Fit Index (CFI) 0.860
## Robust Tucker-Lewis Index (TLI) 0.819
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -10550.161 -10550.161
## Loglikelihood unrestricted model (H1) -10449.603 -10449.603
##
## Akaike (AIC) 21154.322 21154.322
## Bayesian (BIC) 21272.263 21272.263
## Sample-size adjusted Bayesian (BIC) 21186.548 21186.548
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.071 0.067
## 90 Percent confidence interval - lower 0.061 0.057
## 90 Percent confidence interval - upper 0.082 0.077
## P-value RMSEA <= 0.05 0.000 0.003
##
## Robust RMSEA 0.070
## 90 Percent confidence interval - lower 0.059
## 90 Percent confidence interval - upper 0.081
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.066 0.066
##
## Parameter Estimates:
##
## Standard errors Robust.sem
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## op =~
## Opene_1 0.621 0.075 8.229 0.000 0.626 0.458
## Opene_2 0.837 0.083 10.037 0.000 0.843 0.607
## Opene_3 0.412 0.064 6.447 0.000 0.415 0.339
## Opene_4 0.798 0.090 8.860 0.000 0.804 0.493
## ag =~
## Agree_1 0.415 0.049 8.415 0.000 0.418 0.443
## Agree_2 0.535 0.049 10.887 0.000 0.539 0.571
## Agree_3 0.678 0.046 14.868 0.000 0.684 0.755
## Agree_4 0.569 0.049 11.534 0.000 0.574 0.648
## ne =~
## Neuro_1 0.718 0.055 13.118 0.000 0.718 0.598
## Neuro_2 0.551 0.055 9.989 0.000 0.551 0.456
## Neuro_3 0.945 0.056 16.749 0.000 0.945 0.731
## Neuro_4 0.735 0.057 12.863 0.000 0.735 0.588
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## ag ~
## ne -0.126 0.060 -2.097 0.036 -0.125 -0.125
## op ~
## ne -0.122 0.068 -1.783 0.075 -0.121 -0.121
## ag 0.005 0.064 0.071 0.943 0.005 0.005
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .Opene_1 1.478 0.105 14.082 0.000 1.478 0.791
## .Opene_2 1.215 0.134 9.043 0.000 1.215 0.631
## .Opene_3 1.328 0.074 17.994 0.000 1.328 0.885
## .Opene_4 2.012 0.147 13.716 0.000 2.012 0.757
## .Agree_1 0.717 0.081 8.825 0.000 0.717 0.804
## .Agree_2 0.601 0.066 9.170 0.000 0.601 0.674
## .Agree_3 0.353 0.052 6.730 0.000 0.353 0.430
## .Agree_4 0.456 0.069 6.583 0.000 0.456 0.581
## .Neuro_1 0.927 0.076 12.258 0.000 0.927 0.642
## .Neuro_2 1.153 0.075 15.312 0.000 1.153 0.792
## .Neuro_3 0.779 0.095 8.194 0.000 0.779 0.466
## .Neuro_4 1.024 0.080 12.881 0.000 1.024 0.655
## .op 1.000 0.985 0.985
## .ag 1.000 0.984 0.984
## ne 1.000 1.000 1.000
##
## R-Square:
## Estimate
## Opene_1 0.209
## Opene_2 0.369
## Opene_3 0.115
## Opene_4 0.243
## Agree_1 0.196
## Agree_2 0.326
## Agree_3 0.570
## Agree_4 0.419
## Neuro_1 0.358
## Neuro_2 0.208
## Neuro_3 0.534
## Neuro_4 0.345
## op 0.015
## ag 0.016
Plot the model
Can use sempaths to plot a model but it’s a mess by deault and usually needs a lot of tweaking to work.
For simple models it works quite well and gives a good overview if everything “works” as expected.
library(semPlot)
semPaths(fit, style = "lisrel", whatLabels= "std", nCharNodes = 0, edge.label.cex= 0.6,
rotation= 2, layout = "tree", label.cex=1, sizeMan = 5, sizeLat = 8)
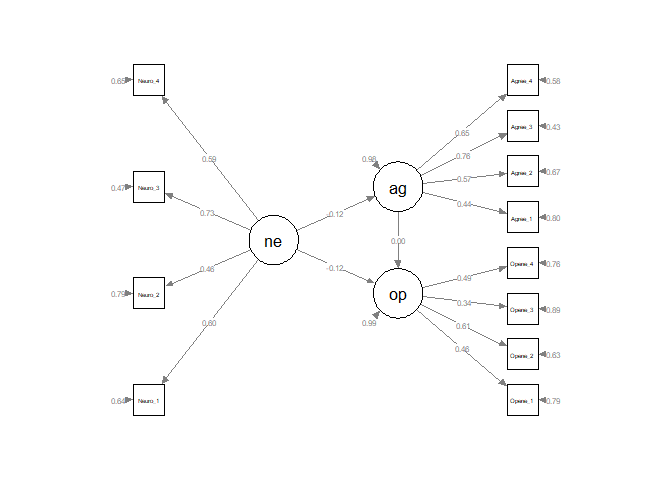
Indirect effects: Mediation
Mediation testing is quite simple in lavaan. Just define the paths you are interested in.
Use the same Assumption testing as before
I use the same model as before “ne -> ag -> op”.
I give variables a label.
model2 <- '
#constructs
op =~ Opene_1 + Opene_2 + Opene_3 + Opene_4
ag =~ Agree_1 + Agree_2 + Agree_3 + Agree_4
ne =~ Neuro_1 + Neuro_2 + Neuro_3 + Neuro_4
#regression
ag ~ c*ne
op ~a*ne + b*ag
#indirect
indirect := a*b
#direct effect
direct := c
#total effect
total := c + (a*b)'
Fit and summary
Fit the model with same parameters as for cfa works and show summary. I shortened the output:
fit2 <- cfa(model2, data=dat, estimator="MLM", std.lv=TRUE)
summary(fit2, fit.measures=T, standardized=T, rsquare=T)
## lavaan 0.6-9 ended normally after 29 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 27
##
## Used Total
## Number of observations 583 600
##
## Model Test User Model:
## Standard Robust
## Test Statistic 201.116 184.729
## Degrees of freedom 51 51
## P-value (Chi-square) 0.000 0.000
## Scaling correction factor 1.089
## Satorra-Bentler correction
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## op =~
## Opene_1 0.621 0.075 8.229 0.000 0.626 0.458
## Opene_2 0.837 0.083 10.037 0.000 0.843 0.607
## Opene_3 0.412 0.064 6.447 0.000 0.415 0.339
## Opene_4 0.798 0.090 8.860 0.000 0.804 0.493
## ag =~
## Agree_1 0.415 0.049 8.415 0.000 0.418 0.443
## Agree_2 0.535 0.049 10.887 0.000 0.539 0.571
## Agree_3 0.678 0.046 14.868 0.000 0.684 0.755
## Agree_4 0.569 0.049 11.534 0.000 0.574 0.648
## ne =~
## Neuro_1 0.718 0.055 13.118 0.000 0.718 0.598
## Neuro_2 0.551 0.055 9.989 0.000 0.551 0.456
## Neuro_3 0.945 0.056 16.749 0.000 0.945 0.731
## Neuro_4 0.735 0.057 12.863 0.000 0.735 0.588
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## ag ~
## ne (c) -0.126 0.060 -2.097 0.036 -0.125 -0.125
## op ~
## ne (a) -0.122 0.068 -1.783 0.075 -0.121 -0.121
## ag (b) 0.005 0.064 0.071 0.943 0.005 0.005
Interaction effects: “Moderation”
Basic interaction term with “:” in lavaan. But it only works with manifest variables. You could also do a quick lm model with m <- lm(y ~ r * s, data=d) See here how to use lm interaction regarding referece groups.
Be carefull not to interpret the main effect of the interaction term in the the model with the interaction present. Here, the baseline of the second IV is dependent on the intercept of the first IV.
When an observed moderator is categorical, maybe use a multigroup in lavaan or just use lm: group=“experience”.
When using latent variables it’s more complicated.
I will follow product-indicator approach for latent interaction.Demonstarted by Schoemann & Jorgensen (2021) https://doi.org/10.3390/psych3030024 Caveat: Croduct indicators are assumed to be continuous if categorial use grouping.
Optional: Rename
Rename vars to be more easy 1 char + int (i.e., a1, a2, a3, b1, b2, b3..).Use the rename function
library(tidyverse)
dat2 <- rename(dat, a1 = ali1)
Import example dataset
dat <- read.csv("exampleMod.csv")
Libraries
library(lavaan)
library(semTools)
Main effects
First step is to check for a main effect:
mMe <- '
tvalue =~ t1 + t2 + t3 + t4
sources =~ s1 + s2 + s3 + s4 + s5
tip =~ tip1 + tip2 + tip3
tip ~ tvalue + sources'
Fit and summary
I shortened the output:
fitME <- sem(mMe, data = dat, std.lv = TRUE, estimator = "mlr")
summary(fitME, fit.measure = F, standardized=T)
## lavaan 0.6-9 ended normally after 22 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 27
##
## Used Total
## Number of observations 7037 7314
##
## Model Test User Model:
## Standard Robust
## Test Statistic 1261.996 1121.253
## Degrees of freedom 51 51
## P-value (Chi-square) 0.000 0.000
## Scaling correction factor 1.126
## Yuan-Bentler correction (Mplus variant)
##
## Parameter Estimates:
##
## Standard errors Sandwich
## Information bread Observed
## Observed information based on Hessian
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## tvalue =~
## t1 0.866 0.010 85.682 0.000 0.866 0.849
## t2 0.856 0.010 85.422 0.000 0.856 0.890
## t3 0.700 0.011 63.669 0.000 0.700 0.769
## t4 0.565 0.013 44.164 0.000 0.565 0.516
## sources =~
## s1 0.757 0.015 50.069 0.000 0.757 0.687
## s2 0.881 0.013 65.982 0.000 0.881 0.719
## s3 0.651 0.014 45.536 0.000 0.651 0.545
## s4 0.732 0.016 45.877 0.000 0.732 0.674
## s5 0.969 0.013 72.537 0.000 0.969 0.795
## tip =~
## tip1 0.585 0.018 32.832 0.000 0.733 0.649
## tip2 0.174 0.013 13.531 0.000 0.218 0.215
## tip3 0.573 0.017 33.179 0.000 0.718 0.631
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## tip ~
## tvalue -0.118 0.022 -5.315 0.000 -0.094 -0.094
## sources 0.724 0.030 23.933 0.000 0.578 0.578
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## tvalue ~~
## sources -0.191 0.015 -12.819 0.000 -0.191 -0.191
Both main effects are significant.
Higher test value -> lower fear appeal. More sources of teacher stress -> higher fear appeal.
Data prep
Use the indProd() function in the semTools to create new dataset with multiplied x and z vars. var1 = indicators…
var2 = moderator vars
var3 = optional vars for three way interaction
Can use meanC, residualC, and doubleMC centering approach. Schoemann & Jorgensen use DMC or residual.
This will create a new dataset with multiplied variables named t1.s1, t1.s2…
dat2 <- indProd(dat, var1 = c("t1", "t2", "t3", "t4"),
var2 = c("s1", "s2", "s3", "s4", "s5"),
match = F, meanC = F, residualC = T)
Specify the model
First latent factors; 0* covariances with interaction; regression paths; residual covariances.
Do covariances in blocks first horizontally and then vertically.
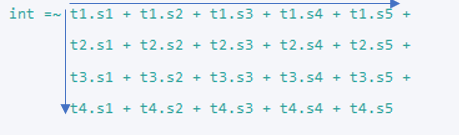
Use Notepad replace function to speed up the writing.
model <- '
tvalue =~ t1 + t2 + t3 + t4
sources =~ s1 + s2 + s3 + s4 + s5
tip =~ tip1 + tip2 + tip3
int =~ t1.s1 + t1.s2 + t1.s3 + t1.s4 + t1.s5 +
t2.s1 + t2.s2 + t2.s3 + t2.s4 + t2.s5 +
t3.s1 + t3.s2 + t3.s3 + t3.s4 + t3.s5 +
t4.s1 + t4.s2 + t4.s3 + t4.s4 + t4.s5
#Fix covariances between interaction and predictors to 0
tvalue ~~ 0*int
sources ~~ 0*int
#regression paths
tip ~ tvalue + sources + int
#Residual covariances between terms from the same indicator
#Do covariances horizontally -> and vertically I
#horizontally
t1.s1 ~~ th1*t1.s2 + th1*t1.s3 + th1*t1.s4 + th1*t1.s5
t1.s2 ~~ th1*t1.s3 + th1*t1.s4 + th1*t1.s5
t1.s3 ~~ th1*t1.s4 + th1*t1.s5
t1.s4 ~~ th1*t1.s5
t2.s1 ~~ th2*t2.s2 + th2*t2.s3 + th2*t2.s4 + th2*t2.s5
t2.s2 ~~ th2*t2.s3 + th2*t2.s4 + th2*t2.s5
t2.s3 ~~ th2*t2.s4 + th2*t2.s5
t2.s4 ~~ th2*t2.s5
t3.s1 ~~ th3*t3.s2 + th3*t3.s3 + th3*t3.s4 + th3*t3.s5
t3.s2 ~~ th3*t3.s3 + th3*t3.s4 + th3*t3.s5
t3.s3 ~~ th3*t3.s4 + th3*t3.s5
t3.s4 ~~ th3*t3.s5
t4.s1 ~~ th4*t4.s2 + th4*t4.s3 + th4*t4.s4 + th4*t4.s5
t4.s2 ~~ th4*t4.s3 + th4*t4.s4 + th4*t4.s5
t4.s3 ~~ th4*t4.s4 + th4*t4.s5
t4.s4 ~~ th4*t4.s5
#vertically
t1.s1 ~~ th5*t2.s1 + th5*t3.s1 + th5*t4.s1
t2.s1 ~~ th5*t3.s1 + th5*t4.s1
t3.s1 ~~ th5*t4.s1
t1.s2 ~~ th6*t2.s2 + th6*t3.s2 + th6*t4.s2
t2.s2 ~~ th6*t3.s2 + th6*t4.s2
t3.s2 ~~ th6*t4.s2
t1.s3 ~~ th7*t2.s3 + th7*t3.s3 + th7*t4.s3
t2.s3 ~~ th7*t3.s3 + th7*t4.s3
t3.s3 ~~ th7*t4.s3
t1.s4 ~~ th8*t2.s4 + th8*t3.s4 + th8*t4.s4
t2.s4 ~~ th8*t3.s4 + th8*t4.s4
t3.s4 ~~ th8*t4.s4
t1.s5 ~~ th9*t2.s5 + th9*t3.s5 + th9*t4.s5
t2.s5 ~~ th9*t3.s5 + th9*t4.s5
t3.s5 ~~ th9*t4.s5
'
Fit and summary
I shortened the output:
fit <- sem(model, data = dat2, std.lv = TRUE, meanstructure = TRUE)
summary(fit, fit.measure = F, standardized = TRUE)
## lavaan 0.6-9 ended normally after 51 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 170
## Number of equality constraints 61
##
## Used Total
## Number of observations 7037 7314
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## tvalue =~
## t1 0.866 0.010 83.934 0.000 0.866 0.849
## t2 0.856 0.010 89.777 0.000 0.856 0.890
## t3 0.700 0.010 73.141 0.000 0.700 0.769
## t4 0.565 0.013 44.117 0.000 0.565 0.516
## sources =~
## s1 0.757 0.012 60.565 0.000 0.757 0.687
## s2 0.881 0.014 64.360 0.000 0.881 0.719
## s3 0.651 0.014 45.599 0.000 0.651 0.545
## s4 0.732 0.012 59.161 0.000 0.732 0.674
## s5 0.969 0.013 73.532 0.000 0.969 0.795
## tip =~
## tip1 0.582 0.016 36.641 0.000 0.731 0.648
## tip2 0.173 0.012 14.434 0.000 0.218 0.214
## tip3 0.572 0.016 36.646 0.000 0.719 0.633
## int =~
## t1.s1 0.669 0.014 46.845 0.000 0.669 0.578
## t1.s2 0.873 0.015 58.513 0.000 0.873 0.688
## t1.s3 0.591 0.015 38.633 0.000 0.591 0.491
## t1.s4 0.686 0.014 48.809 0.000 0.686 0.598
## t1.s5 0.961 0.015 65.346 0.000 0.961 0.748
## t2.s1 0.663 0.014 48.642 0.000 0.663 0.598
## t2.s2 0.848 0.014 60.113 0.000 0.848 0.704
## t2.s3 0.587 0.015 40.434 0.000 0.587 0.512
## t2.s4 0.677 0.014 50.017 0.000 0.677 0.611
## t2.s5 0.938 0.014 67.637 0.000 0.938 0.768
## t3.s1 0.537 0.014 38.354 0.000 0.537 0.484
## t3.s2 0.664 0.014 46.262 0.000 0.664 0.572
## t3.s3 0.483 0.015 32.158 0.000 0.483 0.413
## t3.s4 0.554 0.014 40.398 0.000 0.554 0.507
## t3.s5 0.745 0.014 52.698 0.000 0.745 0.641
## t4.s1 0.413 0.018 23.517 0.000 0.413 0.309
## t4.s2 0.501 0.019 27.030 0.000 0.501 0.355
## t4.s3 0.374 0.020 18.941 0.000 0.374 0.251
## t4.s4 0.444 0.017 25.668 0.000 0.444 0.336
## t4.s5 0.569 0.018 32.100 0.000 0.569 0.420
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## tip ~
## tvalue -0.117 0.019 -6.070 0.000 -0.094 -0.094
## sources 0.726 0.027 27.293 0.000 0.578 0.578
## int -0.069 0.020 -3.442 0.001 -0.055 -0.055
##
Plot the model
library(semPlot)
semPaths(fit, style = "lisrel", whatLabels= "std", nCharNodes = 0, edge.label.cex= 0.6,
rotation= 2, layout = "tree", label.cex=0.9, sizeMan = 4, sizeLat = 5, residuals=F)
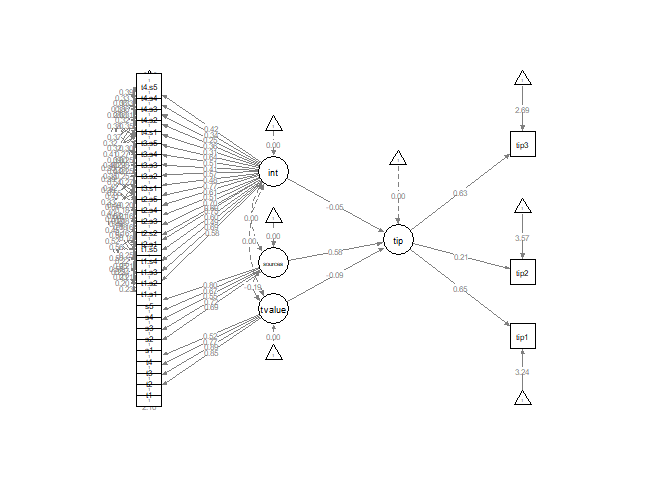
Plot the interaction
Find slopes for plot interaction via probe function.
USE differnt probe functions for two and tree way interaction, and different centering techniques!!
You can do more interaction values valProbe = c(-3,0,3…)). Sufficient to do 3 simple slopes at the 1 SD below the mean of var (−1), the mean of var (0), and 1 SD above the mean of var (1).
pRC <- probe2WayRC(fit, nameX = c("tvalue", "sources", "int"),
nameY = "tip", modVar = "tvalue",
valProbe = c(-2,-1,0,1,2))
#plot the interaction graph
plotProbe(pRC, xlim = c(-2,2), xlab = "Sources of teacher stress", ylab = "Fear Appeals",
legendArgs = list(title = "Test Value"))
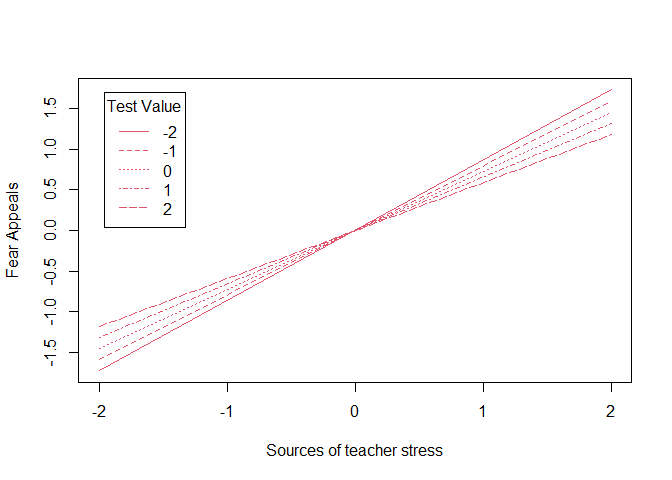
Interpretation
Main and interaction effects are significant. Higher test value -> lower fear appeal; More sources of teacher stress -> higher fear appeal; Interaction: test value reduces the negative positive effect of sources on fear.
Test multiple models in a row
This is a little example to specify a model and then change the name of the predictor then test each model individually.
library(lavaan)
#create random dataset
x <- sample(0:10, 1000, rep = TRUE)
y <- sample(0:10, 1000, rep = TRUE)
x2<- sample(0:10, 1000, rep = TRUE)
x3<- sample(0:10, 1000, rep = TRUE)
f <- data.frame(x,x2,x3,y)
#this is the model, I want to iterate on
model <- 'y ~ pred'
#these are the x vars I want to test as predictors
preds <- c("x", "x2", "x3")
#function to replace the word pred with list in preds
fx <- function(x) {
model <- str_replace_all(model, "pred", x)
return(model)
}
#this generates a list of models for all preds
models <- lapply(preds, FUN = fx)
#this runs every model and stores them in the object fit
fit <- list()
for(i in seq_along(models)) {
fit[[i]] <- sem(models[[i]], f)
}
#rename list to predictors
names(fit) <- preds
#move to global vars
list2env(fit, globalenv())
#sumamry(x)
#sumamry(x2)
#sumamry(x3)
In this example, I change “pred” and “outcome” to generate 15 models
# These are the x vars I want to test as predictors
preds <- c("auton", "compe", "relat")
# These are the y vars I want to test as outcomes
outs <- c("bat", "bat_exhaus", "bat_psydis", "bat_emocont", "bat_cogcont")
# In total this creates 15 models, name the models
mnames <- c(c(paste0(preds, outs[1])), c(paste0(preds, outs[2])), c(paste0(preds, outs[3])),
c(paste0(preds, outs[4])),c(paste0(preds, outs[5])))
# Function to replace the word "pred" with list in relats
fx <- function(x) {
model <- str_replace_all(model, "pred", x)
return(model)
}
# This generates a list of models for all preds
models <- lapply(preds, FUN = fx)
# Generate a model for each outcome
fy <- function(x) {
models <- str_replace_all(models, "out", x)
return(models)
}
models <- lapply(outs, FUN = fy)
models <- flatten(models)
# Name modelsin the list
names(models) <- mnames
# Generate a object for each list element in the global env
list2env(models, globalenv())