Navigation Structure
Table of contents
Prerequisites
Load required packages:
#import libraries
library(MVN)
library(lavaan)
library(foreign)
library(tidyverse)
library(psych)
library(semPlot)
library(semTools)
library(apaTables)
Import our dataset:
#import data
dat <- read.table("uk_ipip300_data1.csv", sep = ";", header = TRUE)
CFA: Second order
Assumption testing
Test for multivariate normality:
#First: new dataset with variables of interest
extra.labels <- c("Opene_1", "Opene_2", "Opene_3", "Opene_4",
"Agree_1", "Agree_2", "Agree_3", "Agree_4",
"Neuro_1", "Neuro_2", "Neuro_3", "Neuro_4")
dat.extra <- na.omit(dat[,extra.labels])
# MVN command for QQ-Plot, Normality tests
mvn(dat.extra, mvnTest = c("mardia"), multivariatePlot = "qq", desc = F)
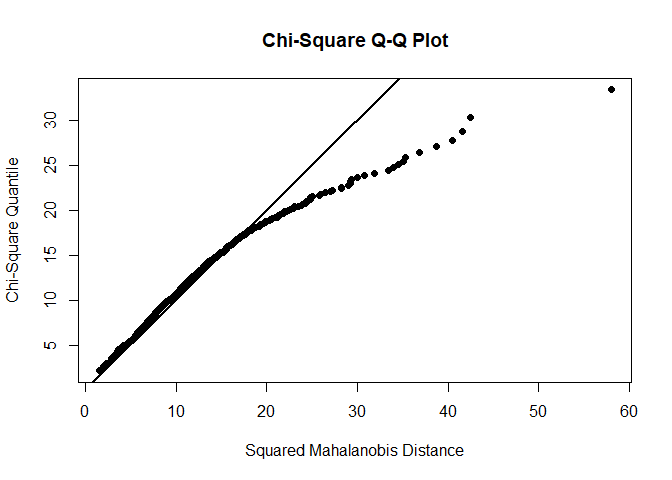
## $multivariateNormality
## Test Statistic p value Result
## 1 Mardia Skewness 1244.98550356253 9.57858038202079e-97 NO
## 2 Mardia Kurtosis 12.7621671073881 0 NO
## 3 MVN <NA> <NA> NO
##
## $univariateNormality
## Test Variable Statistic p value Normality
## 1 Anderson-Darling Opene_1 21.1669 <0.001 NO
## 2 Anderson-Darling Opene_2 23.5159 <0.001 NO
## 3 Anderson-Darling Opene_3 18.9456 <0.001 NO
## 4 Anderson-Darling Opene_4 44.2574 <0.001 NO
## 5 Anderson-Darling Agree_1 43.6023 <0.001 NO
## 6 Anderson-Darling Agree_2 39.9714 <0.001 NO
## 7 Anderson-Darling Agree_3 39.9981 <0.001 NO
## 8 Anderson-Darling Agree_4 47.9344 <0.001 NO
## 9 Anderson-Darling Neuro_1 19.3713 <0.001 NO
## 10 Anderson-Darling Neuro_2 25.3773 <0.001 NO
## 11 Anderson-Darling Neuro_3 20.8063 <0.001 NO
## 12 Anderson-Darling Neuro_4 21.7073 <0.001 NO
##
## $multivariateOutliers
## NULL
Next check for multivariate outliers: See here how to check for outliers (Leverage / Influence).
Specify model
We specify a second order model with three first order factors:
pers <- '
pers =~ op + ag + ne
op =~ Opene_1 + Opene_2 + Opene_3 + Opene_4
ag =~ Agree_1 + Agree_2 + Agree_3 + Agree_4
ne =~ Neuro_1 + Neuro_2 + Neuro_3 + Neuro_4'
And we specify a first order model just for fun:
pers1 <- '
op =~ Opene_1 + Opene_2 + Opene_3 + Opene_4
ag =~ Agree_1 + Agree_2 + Agree_3 + Agree_4
ne =~ Neuro_1 + Neuro_2 + Neuro_3 + Neuro_4'
Fit the model
Use MLM or MLR with missings.
fit.cfa.pers <- cfa(pers, data=dat, estimator ="MLM", std.lv=TRUE)
Fit first order cfa:
fit.cfa.pers1 <- cfa(pers1, data=dat, estimator ="MLM", std.lv=TRUE)
Plot the model
semPaths(fit.cfa.pers, style = "lisrel", whatLabels= "std", nCharNodes = 0, edge.label.cex= 0.6,
rotation= 2, layout = "tree2", label.cex=1, sizeMan = 5, sizeLat = 8)
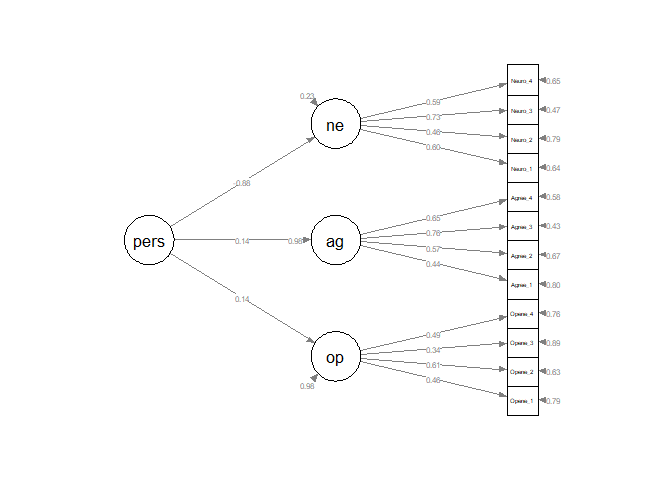
Output
summary(fit.cfa.pers, standardized= TRUE, fit.measures=TRUE)
## lavaan 0.6-9 ended normally after 88 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 27
##
## Used Total
## Number of observations 583 600
##
## Model Test User Model:
## Standard Robust
## Test Statistic 201.116 184.729
## Degrees of freedom 51 51
## P-value (Chi-square) 0.000 0.000
## Scaling correction factor 1.089
## Satorra-Bentler correction
##
## Model Test Baseline Model:
##
## Test statistic 1111.634 1002.792
## Degrees of freedom 66 66
## P-value 0.000 0.000
## Scaling correction factor 1.109
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.856 0.857
## Tucker-Lewis Index (TLI) 0.814 0.815
##
## Robust Comparative Fit Index (CFI) 0.860
## Robust Tucker-Lewis Index (TLI) 0.819
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -10550.161 -10550.161
## Loglikelihood unrestricted model (H1) -10449.603 -10449.603
##
## Akaike (AIC) 21154.322 21154.322
## Bayesian (BIC) 21272.263 21272.263
## Sample-size adjusted Bayesian (BIC) 21186.548 21186.548
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.071 0.067
## 90 Percent confidence interval - lower 0.061 0.057
## 90 Percent confidence interval - upper 0.082 0.077
## P-value RMSEA <= 0.05 0.000 0.003
##
## Robust RMSEA 0.070
## 90 Percent confidence interval - lower 0.059
## 90 Percent confidence interval - upper 0.081
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.066 0.066
##
## Parameter Estimates:
##
## Standard errors Robust.sem
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## pers =~
## op 0.140 0.241 0.581 0.561 0.138 0.138
## ag 0.143 0.246 0.582 0.561 0.142 0.142
## ne -1.836 12.928 -0.142 0.887 -0.878 -0.878
## op =~
## Opene_1 0.620 0.079 7.847 0.000 0.626 0.458
## Opene_2 0.835 0.086 9.659 0.000 0.843 0.607
## Opene_3 0.411 0.063 6.495 0.000 0.415 0.339
## Opene_4 0.796 0.097 8.231 0.000 0.804 0.493
## ag =~
## Agree_1 0.414 0.050 8.272 0.000 0.418 0.443
## Agree_2 0.534 0.051 10.400 0.000 0.539 0.571
## Agree_3 0.677 0.050 13.423 0.000 0.684 0.755
## Agree_4 0.568 0.050 11.410 0.000 0.574 0.648
## ne =~
## Neuro_1 0.344 1.867 0.184 0.854 0.718 0.598
## Neuro_2 0.263 1.432 0.184 0.854 0.551 0.456
## Neuro_3 0.452 2.455 0.184 0.854 0.945 0.731
## Neuro_4 0.352 1.910 0.184 0.854 0.735 0.588
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .Opene_1 1.478 0.105 14.082 0.000 1.478 0.791
## .Opene_2 1.215 0.134 9.043 0.000 1.215 0.631
## .Opene_3 1.328 0.074 17.994 0.000 1.328 0.885
## .Opene_4 2.012 0.147 13.716 0.000 2.012 0.757
## .Agree_1 0.717 0.081 8.825 0.000 0.717 0.804
## .Agree_2 0.601 0.066 9.170 0.000 0.601 0.674
## .Agree_3 0.353 0.052 6.730 0.000 0.353 0.430
## .Agree_4 0.456 0.069 6.583 0.000 0.456 0.581
## .Neuro_1 0.927 0.076 12.258 0.000 0.927 0.642
## .Neuro_2 1.153 0.075 15.312 0.000 1.153 0.792
## .Neuro_3 0.779 0.095 8.194 0.000 0.779 0.466
## .Neuro_4 1.024 0.080 12.881 0.000 1.024 0.655
## pers 1.000 1.000 1.000
## .op 1.000 0.981 0.981
## .ag 1.000 0.980 0.980
## .ne 1.000 0.229 0.229
Interpret model fit quickly
With my meval function you can interpret lavaan objects quickly
library(devtools)
source_url("https://lucasmaunz.org/download/meval.R")
meval(fit.cfa.pers)
## $regular
## estimate interpretation
## chisq 201.12 –
## df 51.00 –
## pvalue 0.00 –
## cmin/df 3.94 acceptable
## cfi 0.86 terrible
## tli 0.81 terrible
## rmsea 0.07 acceptable
## srmr 0.07 excellent
##
## $scaled
## estimate interpretation
## chisq.scaled 184.73 –
## df.scaled 51.00 –
## pvalue.scaled 0.00 –
## cmin/df 3.62 acceptable
## cfi.scaled 0.86 terrible
## tli.scaled 0.82 terrible
## rmsea.scaled 0.07 acceptable
## srmr_bentler 0.07 excellent
Modification indices
Print highest modification indices: Maybe covary residuals which highly covary. This is sometimes justified. According to Brown (2015) some of the nonrandom measurement error that should be correlated can be a result of questionnaires, particularly with similar item wordings.
library(lavaan)
fit.cfa.pers.mi <- modificationindices(fit.cfa.pers)
head(fit.cfa.pers.mi[order(fit.cfa.pers.mi$mi, decreasing=TRUE),],25)
## lhs op rhs mi epc sepc.lv sepc.all sepc.nox
## 128 Neuro_1 ~~ Neuro_2 45.160 0.384 0.384 0.371 0.371
## 58 ag =~ Neuro_3 28.517 -0.312 -0.316 -0.244 -0.244
## 131 Neuro_2 ~~ Neuro_3 27.691 -0.372 -0.372 -0.392 -0.392
## 133 Neuro_3 ~~ Neuro_4 22.575 0.464 0.464 0.519 0.519
## 130 Neuro_1 ~~ Neuro_4 19.939 -0.317 -0.317 -0.326 -0.326
## 57 ag =~ Neuro_2 19.906 0.245 0.248 0.205 0.205
## 36 pers =~ Agree_1 19.801 0.224 0.224 0.237 0.237
## 64 ne =~ Agree_1 19.766 -0.094 -0.196 -0.207 -0.207
## 42 pers =~ Neuro_3 16.908 -5.644 -5.644 -4.364 -4.364
## 55 ag =~ Opene_4 16.296 -0.316 -0.319 -0.196 -0.196
## 89 Opene_3 ~~ Opene_4 14.688 -0.353 -0.353 -0.216 -0.216
## 111 Agree_1 ~~ Neuro_3 13.598 -0.144 -0.144 -0.193 -0.193
## 56 ag =~ Neuro_1 13.562 0.195 0.197 0.164 0.164
## 100 Opene_4 ~~ Agree_3 13.547 -0.174 -0.174 -0.206 -0.206
## 68 Opene_1 ~~ Opene_2 12.968 -0.509 -0.509 -0.380 -0.380
## 117 Agree_2 ~~ Neuro_3 11.474 -0.126 -0.126 -0.184 -0.184
## 40 pers =~ Neuro_1 11.311 4.177 4.177 3.477 3.477
## 41 pers =~ Neuro_2 10.377 4.144 4.144 3.434 3.434
## 67 ne =~ Agree_4 10.369 0.060 0.126 0.142 0.142
## 54 ag =~ Opene_3 10.225 0.186 0.188 0.153 0.153
## 39 pers =~ Agree_4 10.086 -0.142 -0.142 -0.160 -0.160
## 93 Opene_3 ~~ Agree_4 9.392 0.113 0.113 0.146 0.146
## 37 pers =~ Agree_2 8.300 0.139 0.139 0.148 0.148
## 65 ne =~ Agree_2 8.100 -0.058 -0.121 -0.128 -0.128
## 70 Opene_1 ~~ Opene_4 6.044 0.320 0.320 0.186 0.186
Reliability
Cronbach’s alpha Bollen (1980), also Raykov (2001) Omega (omega1) Bentler (1972, 2009) Omega (omega2) McDonald Omega (omega3)
Convergent validity: AVE Should be greater than 0.500.
Discriminant validity: Square root of the AVE should be greater than any inter-factor correlations!
library(semTools)
#semTools::reliability(fit.cfa.pers1)
# this is the updated command
compRelSEM(fit.cfa.pers1, higher = "pers")
## op ag ne
## alpha 0.5318028 0.6891802 0.6874082
## omega 0.5449025 0.6975986 0.6914090
## omega2 0.5449025 0.6975986 0.6914090
## omega3 0.5459778 0.6993370 0.6868325
## avevar 0.2414591 0.3724992 0.3672161
Second order reliability: Reliability values at Levels 1 and 2 of the second-order factor, as well as the partial reliability value at Level 1 the “pers” describes the second order factor.
semTools::reliabilityL2(fit.cfa.pers, "pers")
## omegaL1 omegaL2 partialOmegaL1
## 0.1226844 0.4455660 0.2313858
CFA: Bifactor model
The bifactor model hypothesizes a general factor, onto which all items load, and a series of orthogonal (uncorrelated) skill-specific grouping factors. The model is particularly valuable for evaluating the empirical plausibility of subscales and the practical impact of dimensionality assumptions on test scores (Dunn & McCray,2020).
Same assumptions like above.
Specify model
#specify model
pers.bi <- '
pers =~ Opene_1 + Opene_2 + Opene_3 + Opene_4 + Agree_1 + Agree_2 + Agree_3 + Agree_4 + Neuro_1 + Neuro_2 + Neuro_3 + Neuro_4
op =~ Opene_1 + Opene_2 + Opene_3 + Opene_4
ag =~ Agree_1 + Agree_2 + Agree_3 + Agree_4
ne =~ Neuro_1 + Neuro_2 + Neuro_3 + Neuro_4
pers ~~ 0*op + 0*ag + 0*ne
op ~~ 0*ag + 0*ne
ag ~~ 0*ne'
Fit the model
fit.cfa.pers.bi <- cfa(pers.bi, data=dat, estimator ="MLM", std.lv=TRUE)
Plot of model
#First make row order with x= hight, y = width of variable position
x=c(1,2,3,4,5,6,7,8,9,10,11,12,7,3,6,10)
y=c(0,0,0,0,0,0,0,0,0,0,0,0,1,-1,-1,-1)
ly=matrix(c(y,x), ncol=2)
semPaths(fit.cfa.pers.bi, layout=ly, whatLabels="std", style="lisrel", nCharNodes=5, exoCov=FALSE,
residuals=FALSE, label.scale=TRUE, sizeMan2=1.5,
sizeMan=6, asize=1, edge.color="black", edge.label.color="black",
edge.label.position=.8, edge.label.margin=-.1, width=17, height=20)
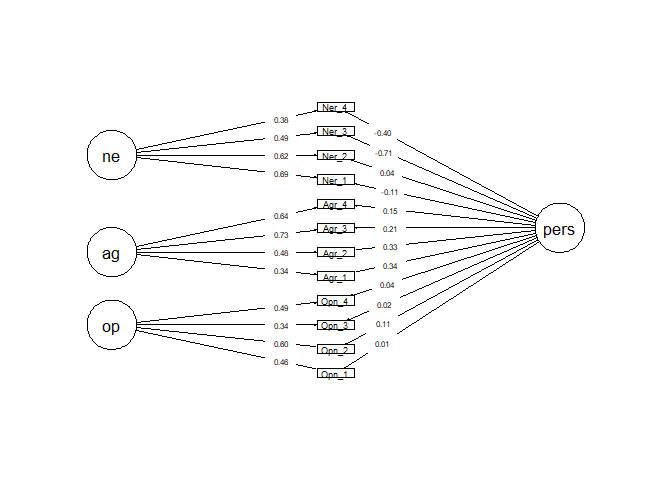
Output
Maybe check modification indicies again after this.
summary(fit.cfa.pers.bi, standardized= TRUE, fit.measures=TRUE)
## lavaan 0.6-9 ended normally after 56 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 36
##
## Used Total
## Number of observations 583 600
##
## Model Test User Model:
## Standard Robust
## Test Statistic 99.253 93.886
## Degrees of freedom 42 42
## P-value (Chi-square) 0.000 0.000
## Scaling correction factor 1.057
## Satorra-Bentler correction
##
## Model Test Baseline Model:
##
## Test statistic 1111.634 1002.792
## Degrees of freedom 66 66
## P-value 0.000 0.000
## Scaling correction factor 1.109
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.945 0.945
## Tucker-Lewis Index (TLI) 0.914 0.913
##
## Robust Comparative Fit Index (CFI) 0.947
## Robust Tucker-Lewis Index (TLI) 0.917
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -10499.229 -10499.229
## Loglikelihood unrestricted model (H1) -10449.603 -10449.603
##
## Akaike (AIC) 21070.459 21070.459
## Bayesian (BIC) 21227.714 21227.714
## Sample-size adjusted Bayesian (BIC) 21113.427 21113.427
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.048 0.046
## 90 Percent confidence interval - lower 0.036 0.034
## 90 Percent confidence interval - upper 0.061 0.058
## P-value RMSEA <= 0.05 0.567 0.689
##
## Robust RMSEA 0.047
## 90 Percent confidence interval - lower 0.035
## 90 Percent confidence interval - upper 0.060
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.048 0.048
##
## Parameter Estimates:
##
## Standard errors Robust.sem
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## pers =~
## Opene_1 0.013 0.072 0.181 0.857 0.013 0.010
## Opene_2 0.151 0.073 2.061 0.039 0.151 0.109
## Opene_3 0.020 0.069 0.293 0.770 0.020 0.017
## Opene_4 0.064 0.085 0.743 0.457 0.064 0.039
## Agree_1 0.321 0.058 5.507 0.000 0.321 0.340
## Agree_2 0.312 0.061 5.111 0.000 0.312 0.331
## Agree_3 0.194 0.052 3.714 0.000 0.194 0.215
## Agree_4 0.137 0.052 2.620 0.009 0.137 0.154
## Neuro_1 -0.135 0.121 -1.117 0.264 -0.135 -0.113
## Neuro_2 0.054 0.117 0.456 0.648 0.054 0.044
## Neuro_3 -0.913 0.118 -7.733 0.000 -0.913 -0.706
## Neuro_4 -0.502 0.103 -4.891 0.000 -0.502 -0.401
## op =~
## Opene_1 0.636 0.075 8.437 0.000 0.636 0.465
## Opene_2 0.830 0.084 9.904 0.000 0.830 0.598
## Opene_3 0.418 0.064 6.568 0.000 0.418 0.341
## Opene_4 0.796 0.092 8.666 0.000 0.796 0.488
## ag =~
## Agree_1 0.323 0.049 6.525 0.000 0.323 0.342
## Agree_2 0.457 0.051 8.898 0.000 0.457 0.484
## Agree_3 0.662 0.053 12.370 0.000 0.662 0.730
## Agree_4 0.569 0.055 10.404 0.000 0.569 0.642
## ne =~
## Neuro_1 0.835 0.093 8.998 0.000 0.835 0.695
## Neuro_2 0.743 0.092 8.074 0.000 0.743 0.615
## Neuro_3 0.636 0.111 5.709 0.000 0.636 0.492
## Neuro_4 0.480 0.081 5.918 0.000 0.480 0.384
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## pers ~~
## op 0.000 0.000 0.000
## ag 0.000 0.000 0.000
## ne 0.000 0.000 0.000
## op ~~
## ag 0.000 0.000 0.000
## ne 0.000 0.000 0.000
## ag ~~
## ne 0.000 0.000 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .Opene_1 1.466 0.105 13.949 0.000 1.466 0.784
## .Opene_2 1.214 0.132 9.182 0.000 1.214 0.631
## .Opene_3 1.325 0.073 18.056 0.000 1.325 0.883
## .Opene_4 2.021 0.147 13.727 0.000 2.021 0.760
## .Agree_1 0.685 0.082 8.359 0.000 0.685 0.768
## .Agree_2 0.585 0.060 9.739 0.000 0.585 0.656
## .Agree_3 0.345 0.058 5.929 0.000 0.345 0.420
## .Agree_4 0.442 0.076 5.849 0.000 0.442 0.563
## .Neuro_1 0.728 0.137 5.328 0.000 0.728 0.504
## .Neuro_2 0.902 0.142 6.369 0.000 0.902 0.619
## .Neuro_3 0.435 0.173 2.506 0.012 0.435 0.260
## .Neuro_4 1.083 0.084 12.962 0.000 1.083 0.692
## pers 1.000 1.000 1.000
## op 1.000 1.000 1.000
## ag 1.000 1.000 1.000
## ne 1.000 1.000 1.000
Interpret model fit quickly
With my meval function you can interpret lavaan objects quickly
library(devtools)
source_url("https://lucasmaunz.org/download/meval.R")
meval(fit.cfa.pers.bi)
## $regular
## estimate interpretation
## chisq 99.25 –
## df 42.00 –
## pvalue 0.00 –
## cmin/df 2.36 excellent
## cfi 0.95 excellent
## tli 0.91 acceptable
## rmsea 0.05 excellent
## srmr 0.05 excellent
##
## $scaled
## estimate interpretation
## chisq.scaled 93.89 –
## df.scaled 42.00 –
## pvalue.scaled 0.00 –
## cmin/df 2.24 excellent
## cfi.scaled 0.94 acceptable
## tli.scaled 0.91 acceptable
## rmsea.scaled 0.05 excellent
## srmr_bentler 0.05 excellent
Easy table of model fits
With this meval.table function you can easily create model fit tables. As input define two vectors, one with models (fitted lavaan objects) and one with names. Specify scaled = T or F. By default regular fits are put out.
# easy table of model fits
# meval.table(models, names)
ms <- c(fit.cfa.pers, fit.cfa.pers.bi)
ns <- c("second order", "bicactor")
mvl <- meval.table(ms, ns, scaled=T)
mvl
#copy table to clipboad and paste into excel
#library(clipr)
#write_clip(mvl)
## chisq.scaled df.scaled cmin/df cfi.scaled rmsea.scaled srmr_bentler
## second order 184.73 51 3.62 0.86 0.07 0.07
## bicactor 93.89 42 2.24 0.94 0.05 0.05
Multilevel CFA (MCFA)
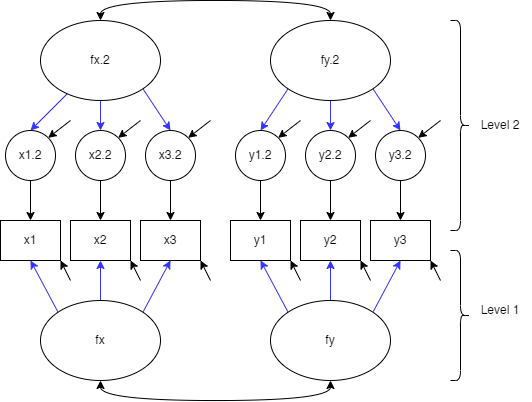
This is basically the same as a normal CFA but we define levels in lavaan. Here is a quick example:
#define the model
mcfa <- '
level: 1
fx =~ x1 + x2 + x3
fy =~ y1 + y2 + y3
level: 2
fx2 =~ x1 + x2 + x3
fy2 =~ y1 + y2 + y3
'
fit <- cfa(mcfa, data = Demo.twolevel, cluster = "cluster")
meval(fit, scaled=F)
## $regular
## estimate interpretation
## chisq 3.22 /
## df 16.00 /
## pvalue 1.00 /
## cmin/df 0.20 excellent
## cfi 1.00 excellent
## tli 1.01 excellent
## rmsea 0.00 excellent
## srmr 0.19 terrible