Navigation Structure
Table of contents
Prerequisites
Load required packages:
#import libraries
library(psych)
library(summarytools)
library(DescTools)
library(effsize)
library(car)
Import our dataset:
#import data
dat <- read.table("stepd.csv", sep = ";", header = TRUE, na = -99)
Data screening
We are interested in the difference between interpersonal problems and gender:
Frequency table
#frequency
freq(dat$gender, order = "freq")
## Frequencies
## dat$gender
## Type: Integer
##
## Freq % Valid % Valid Cum. % Total % Total Cum.
## ----------- ------ --------- -------------- --------- --------------
## 1 100 66.67 66.67 66.67 66.67
## 0 50 33.33 100.00 33.33 100.00
## <NA> 0 0.00 100.00
## Total 150 100.00 100.00 100.00 100.00
Descriptive statistics:
describe(dat$iip_tot)
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 150 86.43 29.71 88.5 86.2 33.36 16 164 148 0.08 -0.39 2.43
Descriptive statistics by group:
describeBy(dat$iip_tot, dat$gender)
##
## Descriptive statistics by group
## group: 0
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 50 81.4 29.54 86 82.78 32.62 16 137 121 -0.35 -0.8 4.18
## ------------------------------------------------------------
## group: 1
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 100 88.95 29.62 90 87.78 31.13 34 164 130 0.29 -0.47 2.96
Plot difference with boxplot:
boxplot(iip_tot ~ gender, data=dat,names=c("male","female"))
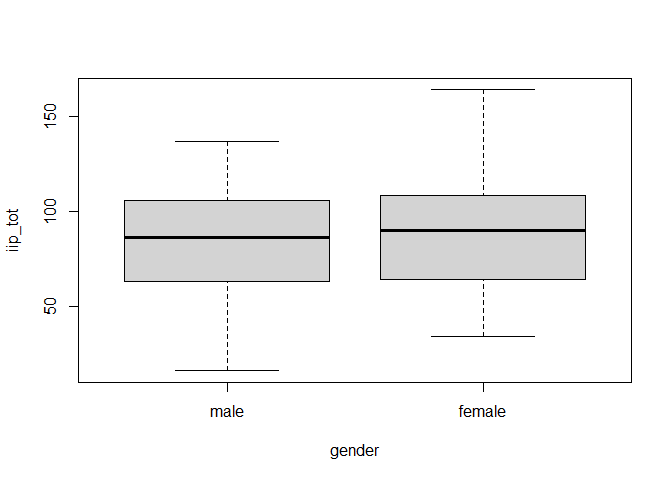
Assumption testing
Normalty test with Shaprio-Wilk test:
Shapiro wilk ns= normal distribution.
shapiro.test(dat$iip_tot)
##
## Shapiro-Wilk normality test
##
## data: dat$iip_tot
## W = 0.9907, p-value = 0.4291
Normalty test with histogram:
hist(dat$iip_tot)
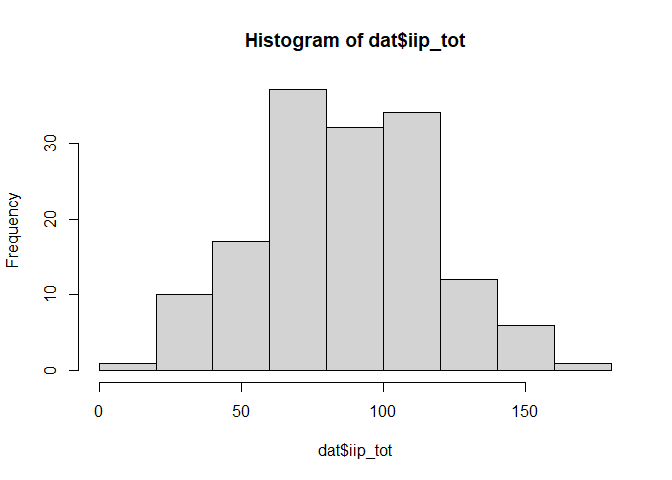
Normalty test with QQ-Plot:
PlotQQ(dat$iip_tot)
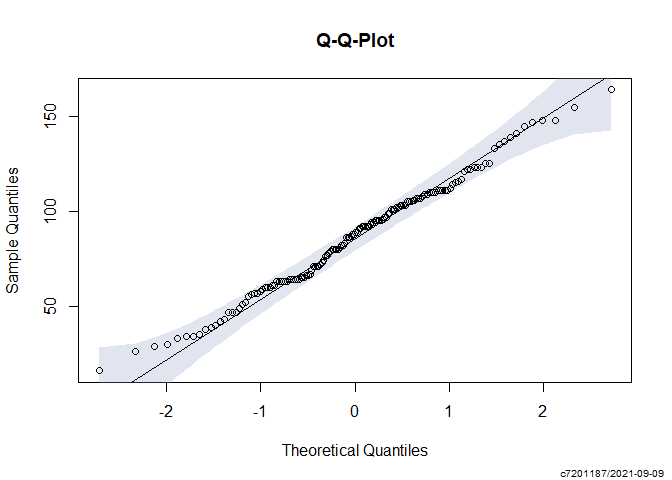
Homogeneity of variance test with lavene test:
Levene test ns= homogeneity.
Later t-test: var.equal = TRUE.
leveneTest(dat$iip_tot, dat$gender)
## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 1 0.0019 0.9649
## 148
T-test
Two sided t-test with homogeneity of variance:
t.test(dat$iip_tot ~ dat$gender, var.equal = TRUE, alternative="two.sided")
##
## Two Sample t-test
##
## data: dat$iip_tot by dat$gender
## t = -1.4731, df = 148, p-value = 0.1428
## alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
## 95 percent confidence interval:
## -17.677849 2.577849
## sample estimates:
## mean in group 0 mean in group 1
## 81.40 88.95
One sided t-test: group 0 > 1.
t.test(dat$iip_tot ~ dat$gender, var.equal = TRUE, alternative="greater")
##
## Two Sample t-test
##
## data: dat$iip_tot by dat$gender
## t = -1.4731, df = 148, p-value = 0.9286
## alternative hypothesis: true difference in means between group 0 and group 1 is greater than 0
## 95 percent confidence interval:
## -16.03316 Inf
## sample estimates:
## mean in group 0 mean in group 1
## 81.40 88.95
One sided t-test: group 0 < 1.
t.test(dat$iip_tot ~ dat$gender, var.equal = TRUE, alternative="less")
##
## Two Sample t-test
##
## data: dat$iip_tot by dat$gender
## t = -1.4731, df = 148, p-value = 0.07142
## alternative hypothesis: true difference in means between group 0 and group 1 is less than 0
## 95 percent confidence interval:
## -Inf 0.9331598
## sample estimates:
## mean in group 0 mean in group 1
## 81.40 88.95
Effect size: cohen’s d:
Cohen 1992
<0.2 negligible
<0.5 small
<0.8 medium
more large
effsize::cohen.d(dat$iip_tot ~ dat$gender, paired = FALSE, na.rm = TRUE)
##
## Cohen's d
##
## d estimate: -0.2551551 (small)
## 95 percent confidence interval:
## lower upper
## -0.59866527 0.08835512
Welch test
Use if variances are not homogenous:
t.test(dat$iip_tot ~ dat$gender, var.equal = F, alternative="two.sided")
##
## Welch Two Sample t-test
##
## data: dat$iip_tot by dat$gender
## t = -1.4745, df = 98.346, p-value = 0.1435
## alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
## 95 percent confidence interval:
## -17.710985 2.610985
## sample estimates:
## mean in group 0 mean in group 1
## 81.40 88.95
Effect size: cohen’s d:
Cohen 1992
<0.2 negligible
<0.5 small
<0.8 medium
more large
cohen.d(dat$iip_tot ~ dat$gender, paired = FALSE, na.rm = TRUE)
##
## Cohen's d
##
## d estimate: -0.2551551 (small)
## 95 percent confidence interval:
## lower upper
## -0.59866527 0.08835512
Mann-Whitney-U test
Use if data is non-normal distributed:
if n<30 exact=T.
wilcox.test(iip_tot~gender, data=dat, exact=FALSE, correct=FALSE, conf.int=FALSE)
##
## Wilcoxon rank sum test
##
## data: iip_tot by gender
## W = 2254.5, p-value = 0.3276
## alternative hypothesis: true location shift is not equal to 0
Effect size U-test: r
z <- qnorm(p)
r <- z/sqrt(N)
Cohen (1992):
r = .10 -> small effect effect
r = .30 -> medium effect
r = .50 -> large effect
w <- wilcox.test(iip_tot~gender, data=dat, exact=FALSE, correct=FALSE, conf.int=FALSE)
f <- freq(dat$gender, order = "freq")
qnorm(w$p.value)/sqrt(f["Total","Freq"])
## [1] -0.03645873