Navigation Structure
Table of contents
Prerequisites
Load required packages:
#import libraries
library(psych)
library(summarytools)
library(car)
library(DescTools)
library(rstatix)
Import our dataset:
#import data
dat <- read.table("stepd2.csv", sep = ";", header = TRUE)
Data screening
We are interested in the difference between problems and experience groups.
Descriptive statistics of variables by Group:
describeBy(dat$iip_tot, dat$exp_content_r)
##
## Descriptive statistics by group
## group: 0
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 57 82.14 28.94 80 81.87 31.13 26 155 129 0.16 -0.3 3.83
## ------------------------------------------------------------
## group: 1
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 34 92.09 24.36 94 92.54 24.46 35 135 100 -0.27 -0.7 4.18
## ------------------------------------------------------------
## group: 2
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 59 87.32 32.91 88 86.55 35.58 16 164 148 0.16 -0.61 4.28
Plot difference:
boxplot(iip_tot ~ exp_content_r, data=dat,names=c("low","mid","high"))
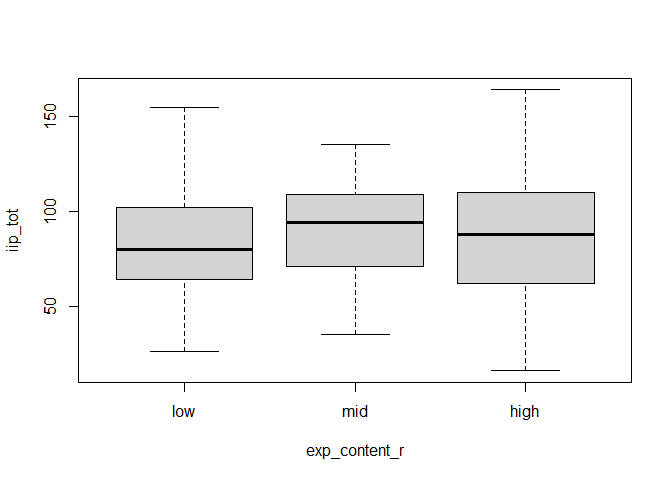
Assumption testing
Normalty test with histogram:
a1 <- aov(dat$iip_tot ~ dat$exp_content_r)
hist(rstandard(a1))
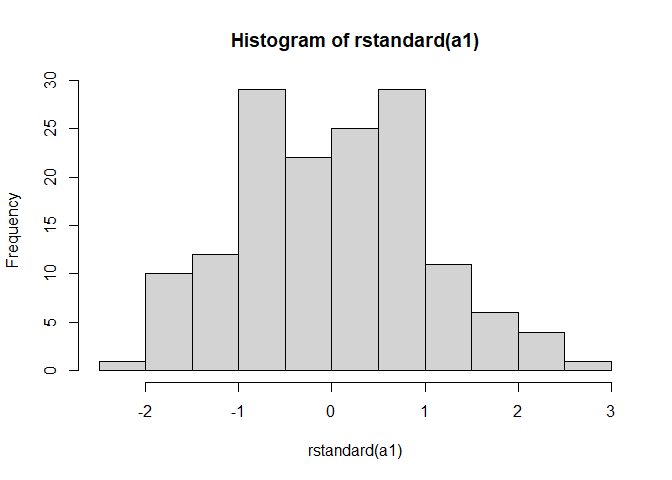
Normalty test with QQ-Plot:
a1 <- aov(dat$iip_tot ~ dat$exp_content_r)
qqPlot(a1)
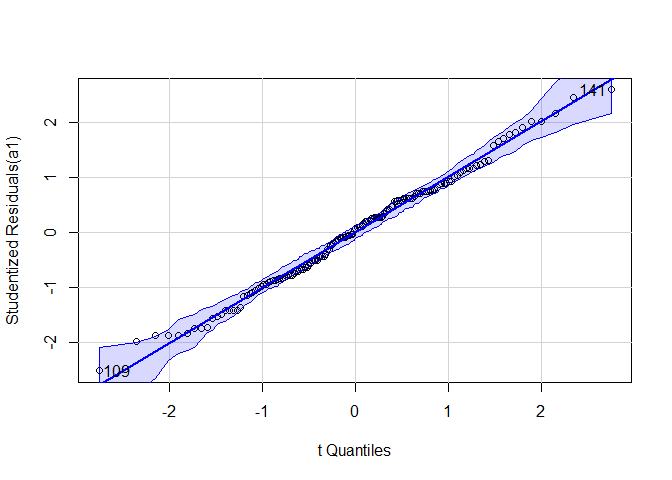
## [1] 109 141
Homogeneity of variance test with lavene test: Levene test ns= homogeneity -> ANOVA.
leveneTest(dat$iip_tot, dat$exp_content_r)
## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 2 1.9693 0.1432
## 147
ANOVA
If assumptions are OK -> ANOVA.
a1 <- aov(dat$iip_tot ~ dat$exp_content_r)
summary(a1)
## Df Sum Sq Mean Sq F value Pr(>F)
## dat$exp_content_r 1 761 761.3 0.862 0.355
## Residuals 148 130722 883.3
Post-hoc analysis:
pairwise.t.test(dat$iip_tot, dat$exp_content_r, p.adjust="bonferroni")
##
## Pairwise comparisons using t tests with pooled SD
##
## data: dat$iip_tot and dat$exp_content_r
##
## 0 1
## 1 0.37 -
## 2 1.00 1.00
##
## P value adjustment method: bonferroni
Effect size:
eta.sq (preferred)
Cohen (1988)
.01 small
.06 medium
.14 large
e <- EtaSq(a1)
e
## eta.sq eta.sq.part
## dat$exp_content_r 0.00578996 0.00578996
Effect size f:
Cohen (1988)
.10 small
.25 medium
.40 large
sqrt(e[1,"eta.sq"]/(1-e[1,"eta.sq"]))
## [1] 0.07631303
Kruskal-Wallis Test
Use if variances are not homogenous / non normal distributed:
kruskal.test(dat$iip_tot ~ dat$exp_content_r)
##
## Kruskal-Wallis rank sum test
##
## data: dat$iip_tot by dat$exp_content_r
## Kruskal-Wallis chi-squared = 2.5004, df = 2, p-value = 0.2865
Post-hoc analysis:
pairwise.wilcox.test(dat$iip_tot, dat$exp_content_r, paired=F, p.adjust="bonferroni")
##
## Pairwise comparisons using Wilcoxon rank sum test with continuity correction
##
## data: dat$iip_tot and dat$exp_content_r
##
## 0 1
## 1 0.32 -
## 2 1.00 1.00
##
## P value adjustment method: bonferroni
Effect size eta.sq:
Cohen (1988)
.01 small
.06 medium
.14 large
dat %>% kruskal_effsize(iip_tot ~ exp_content_r)
## # A tibble: 1 x 5
## .y. n effsize method magnitude
## * <chr> <int> <dbl> <chr> <ord>
## 1 iip_tot 150 0.00340 eta2[H] small